FFT快速傅立叶变换

算法
2.5k 词

众所周知（），FFT凭借如下公式得以实现 现在来谈谈具体的实现问题。

一、单位根的计算

在FFT中，对于下标不同的单位根，可以不用重复计算。此处单位根下标 都是 的幂即 ，因此当 ， ，所以对于下标不同的单位根，有 所以我们仅需计算下标最大的单位根数组 来表示 ，并在需要用到 时使用 即可。

二、系数最终位置的确定

在FFT中，把多项式系数依据奇偶次幂分开进行分治。递归版的FFT中，在函数开头进行分组，每个系数的位置都变化了不止一次，但实际上我们可以一次性完成系数最终位置改变。

考虑第 个元素 表示 系数的数组 ，我们进行一种修改，保留原本偶数项相对顺序，将偶数项移到数组左半边，作为一组；奇数项同样保留原本它们之间的相对顺序，移到右半边，作为另一组。然后再在组内进行此修改直至一组内仅有两个（或一个）元素。

那么对于初始的 ，以下用 代称其内容以防混淆，将 用二进制表示为 ，显然第 次修改时

  • 若 （ 为偶数），则 将在组内的左半边
  • 若 （ 为奇数），则 将在组内的右半边

可以得出，在第 次修改时 （此处修改至每组只有一个元素）

  • 若 （ 在组内的编号为偶数），则 将在组内的左半边
  • 若 （ 在组内的编号为奇数），则 将在组内的右半边

那么 就能表示 的最终位置，如 表示从大到小左半、左半、右半、左半、右半、左半即最终位置为 。现在我们设 最终位置为 ，推导普适结论。

在第 次分组时，每组有两个元素，元素编号从 开始，因此在第 次分组时

  • 若 在左半边，则其位置为
  • 若 在右半边，则其位置为

两者即 。

那么类似地，在第 次分组时

  • 若 在左半边，则
  • 若 在右半边，则

即 （可将 和 视为偏移量系数，偏移 ）。

于是有 ，即 初始位置的逆序为其最终位置。

有了这个结论我们就可以直接从底部开始迭代。

注意若 的二进制逆序为 ，应给交换加上条件 或 ，否则将在遍历到 和 时交换共两次，相当于没有交换。

三、蝴蝶变换

在一般的FFT中，我们这样从底部进行迭代

1
2
3
xa=omega[size/lenth*j]*a[i+j+lenth/2];//lenth 为上次各多项式组的系数个数，size为多项式的总系数个数，i为各组起点，j为组内偏移量
mid[i+j]=a[i+j]+xa;					  //如前面所说，omega[k]为omega(k,size)
mid[i+j+lenth/2]=a[i+j]-xa;

然后在此次变换完成之后将结果储存回数组 

1
a[i+j]=mid[i+j];

需要一个中间数组来储存变换的值。但是蝴蝶变换可以不使用这个中间数组，减少赋值。

由公式可得 到 的部分/全部变换示意图（像个蝴蝶）

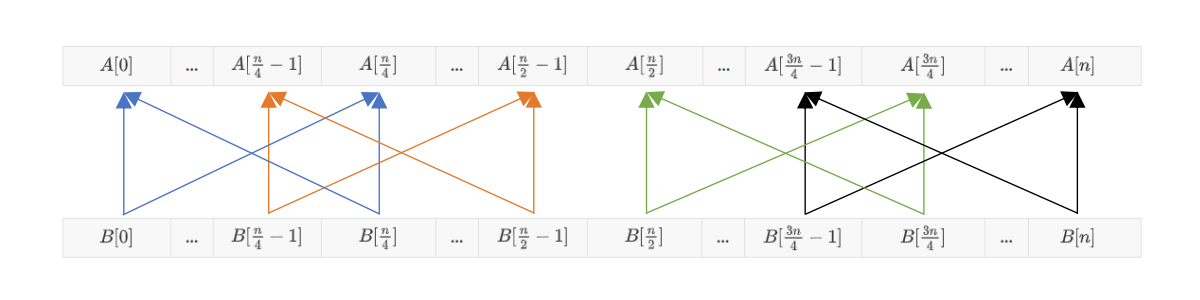
蝴蝶done

可以发现 和 只由 和 决定，并且它们的位置恰好对应。因此我们可以不用中间数组，直接进行赋值迭代

1
2
3
xa=omega[size/lenth*j]*a[i+j+lenth/2];
a[i+j+lenth/2]=a[i+j]+xa;
a[i+j]=a[i+j]+xa;

速度会快一些