ML入门

Coding
8k 词

线性回归

引言

在中学就学习过，一元线性回归中，对于某组常数项和回归系数，有评价标准 使用最小二乘法（正规方程）可以使其最小，此时

多元线性回归

损失函数

类似地，多元线性回归中，对于个样本的个特征 以及一组回归系数，有相同的评价标准，为了去掉样本规模的影响除以，定义损失函数

正规方程

同样可以使用正规方程，求解使得最小。

标量对向量的求导方法

或 依据和形式一致（Denominator Layout）或和形式一致（Numerator Layout）而定，以下采用Denominator Layout。 于是我们有 （或者说，，则）
进一步地，对于二次型

于是

所以 这也就是雅可比矩阵。
二阶导 上面直接认定了代价函数有最小值，在这里我们可以向量对向量求导求海森矩阵 （因为连续函数偏导和求导顺序无关，其海森矩阵是对称矩阵）
而对于任意非零实列向量，的特征值 （内积） 所以是凸函数

令，若可逆，有

带回到一元线性回归

对于 和上文一致。

梯度下降法

就是让某组不断移动一个学习率倍数的偏导，可以进行特征缩放之类的。

联想到seurat

seurat里的特征缩放就是ScaleData()（特征内操作，不过seurat里行名才是特征），还有NormalizeData()的话（样本内操作），会除去不同样本之间数据尺度的影响（测序深度）。

适用于不可逆（一些情况是有特征线性相关，一些情况是样本数太少）以及其它拟合模型等多种情况。

模拟退火！
（注：后来发现，不可逆时损失函数应该仍为凸函数，只是存在一个最低平面，模拟退火用于一些损失函数非凸的模型的梯度下降才更为合适）

逻辑回归

引言

线性回归中，数据沿着拟合的曲线分布。若某曲线为，则和分别代表曲线两边的区域，那有没有一种可能，将数据从曲线两侧分类？逻辑回归就是这么做的。

损失函数

逻辑回归中引入了Sigmoid函数 如此便可以从这条曲线根据或分出正向类和负向类，认为其偏向正向类的概率为。

这时就不能使用线性回归一样的损失函数了。

假如还是使用均方差

一通捣鼓下来算得（可以保留...虽然回头看我算的那一大坨确实算对了） 后面那个是半正定的，，而对于前面

  • 当时，若，这一项为负
  • 当时，若，这一项为负

所以这时损失函数就可能是非凸的，更多的可以看这些回答。

所以我们使用交叉熵损失函数，其中

不行，再这样下去不懂春节期间能不能看完，接下来仅浏览

总之这两种情况可以转化成同一个表达式，然后同样计算海森矩阵，也能发现可以进行凸优化。

决策树

以前一直瞧不起决策树，但是其实人力找出根据特征进行分类的方法是一种更低效的行为...

神经网络

比较好玩的是用神经网络实现逻辑门，比如对于2输入1输出的2层神经网络，输入，连接权值为，输出，即可实现与门，而因为2层网络就只能解决线性可分问题，所以像是XOR、XNOR门就需要构造一下3层的网络。

PS:递归神经网络很适合处理视频这样的时间序列数据，但deeplabcut里面好像没有涉及？我只看到他们多目标的top-down模型（目标识别分割->单独目标姿态识别）的第一步里，声称是使用了前后帧的信息。

PPS:感觉卷积神经网络和动物视觉很像？

聚类

无监督学习之一，让算法自己找出无标记数据集的结构然后把数据点进行分类。一般来说，我们想要簇中的数据点尽可能相似，而簇之间尽可能不同。

介绍一种朴素的方法：K-means，它的想法是指定簇的个数之后，找到个簇的中心（原型），将数据点划分为最近原型对应的簇。（这也就是一种原型聚类，原型是簇的代表）
具体可以这样实现：

  1. 随机选择个数据点作为原型
  2. 迭代：
    1. 将数据点划分为最近原型对应的簇
    2. 更新每个原型为其簇的中心

下面是一个高斯混合分布生成的二维数据的例子：

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np

def kmeans(X, k, max_iter=100, min_change=0):
    m, n = X.shape
    centroids = X[np.random.choice(m, k, replace=False)]
    for _ in range(max_iter):
        cluster = np.argmin(np.linalg.norm(X[:, None] - centroids, axis=2), axis=1)
        centroids_new = np.array([X[cluster == i].mean(axis=0) for i in range(k)])
        if np.all(centroids - centroids_new <= min_change):
            break
        centroids = centroids_new
    return cluster

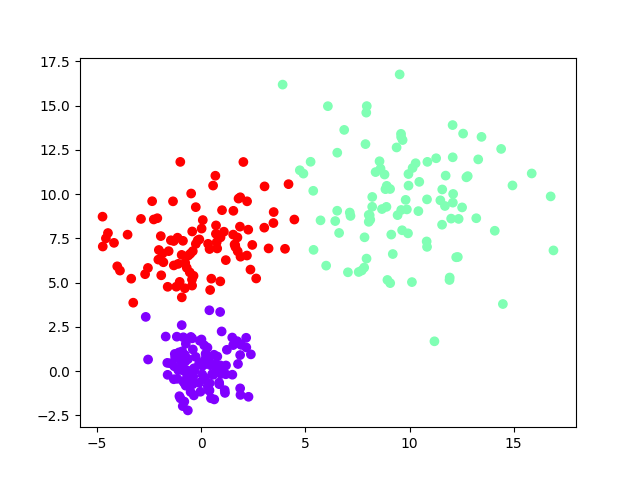
每个簇之间由中心连线的中垂线分隔，很显然这种方法有时无法产生非凸的簇（比如说，一个簇环绕着另一个簇），而且在大簇旁边有小簇的情况下，效果可能并非预期。

这是迭代过程

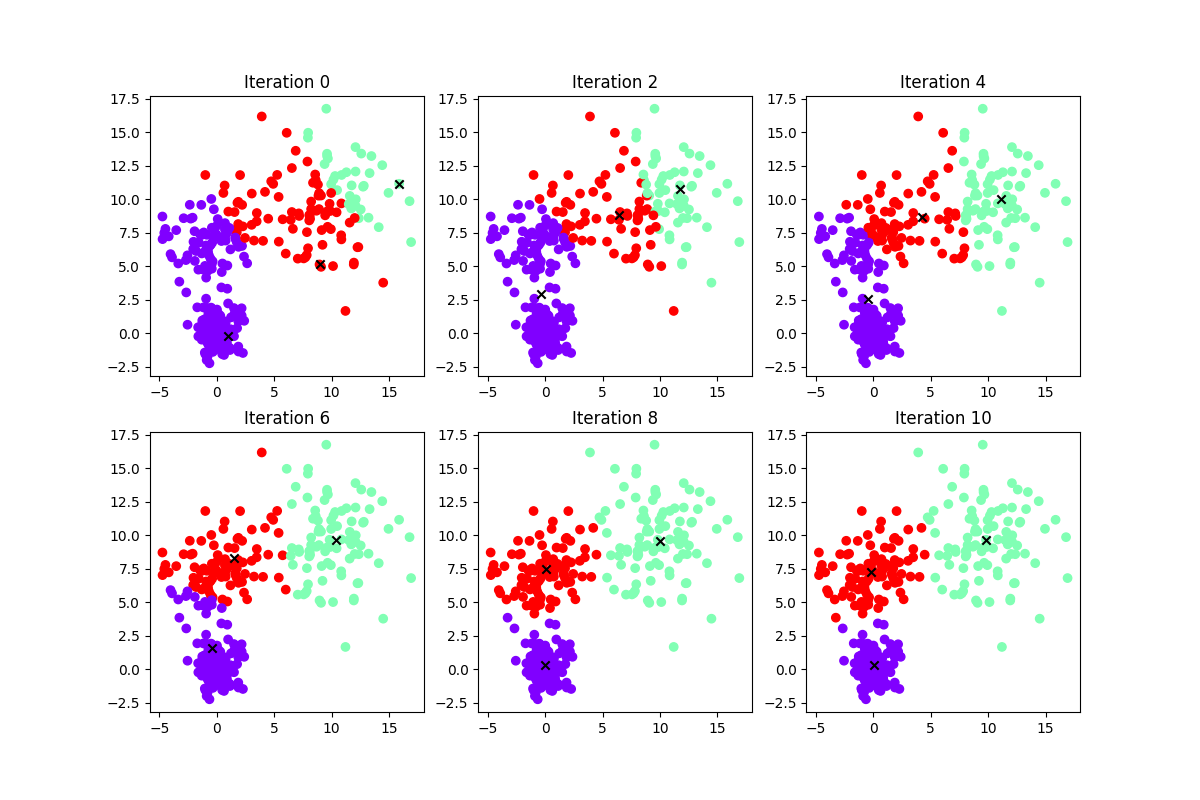
而seurat使用的聚类方法类似于：

  1. 计算k近邻图（k-Nearest Neighbor Graph）：一种朴素的方法是，先计算每个细胞到距离（多种方法）最小的个细胞的有向无权图，然后根据有无边生成无向无权图
  2. 计算共享近邻图（Shared Nearest Neighbor Graph）：对于每条边，计算两端细胞的Jacard相似度（二者共同邻居数/二者总邻居数），生成无向有权图（还可以删掉一些权值较小的边）
  3. 如果使用Louvain算法：初始化每个细胞为一个community，迭代：遍历每个细胞，根据模块度（Modularity）将其贪心地加入相邻community

降维

多维缩放

MDS（骨髓增生异常综合征），目标是将高维的原始样本空间映射到低维的特征空间的同时，尽量保留原始的距离关系。 有两种方式可以实现：

  • 最小化应力函数（样本在低维空间和原始空间的距离差异）
  • 通过原始空间的距离矩阵计算低维空间的内积矩阵，然后进行特征值分解，取最大的几个特征值构成的对角矩阵和相应的特征向量矩阵，计算低维空间的新坐标

主成分分析

在原始空间中找到一些向量构成基的一部分，把数据点投影在这些向量构成的（超）平面上，使用这些向量的线性组合来表示新坐标，其中是每行为一个特征的原始空间，是投影矩阵，有两种指标殊途同归：

  1. 最大化投影后数据点的方差
  2. 最小化投影前后数据点的差异。

最后都能得到最大化。

将原始数据中心化、标准化之后，计算协方差矩阵，可以进行特征值分解，和上面的多维缩放一样取最大的构成投影矩阵；也可以进行奇异值分解得到U和S，取最大的S的成分和对应的U构成投影矩阵，其中可以作为选择个主成分后保留原有方差的比例。